A tunable despeckling neural network stabilized via diffusion equation
| The removal of multiplicative Gamma noise is a critical research area in the application of synthetic aperture radar (SAR) imaging, where neural networks serve as a potent tool. However, real-world data often diverges from theoretical models, exhibiting various disturbances, which makes the neural network less effective. Adversarial attacks can be used as a criterion for judging the adaptability of neural networks to real data, since they can find the most extreme perturbations that make neural networks ineffective. In this work, we propose a tunable, regularized neural network framework that unrolls a shallow neural denoising block and a diffusion regularization block into a single network for end-to-end training. The linear heat equation, known for its inherent smoothness and low-pass filtering properties, is adopted as the diffusion regularization block. The smoothness of our outputs is controlled by a single time step hyperparameter that can be adjusted dynamically. The stability and convergence of our model are theoretically proven. Experimental results demonstrate that the proposed model effectively eliminates high-frequency oscillations induced by adversarial attacks. Finally, the proposed model is benchmarked against several state-of-the-art denoising methods on simulated images, adversarial samples, and real SAR images, achieving superior performance in both quantitative and visual evaluations. Yi Ran et al. | 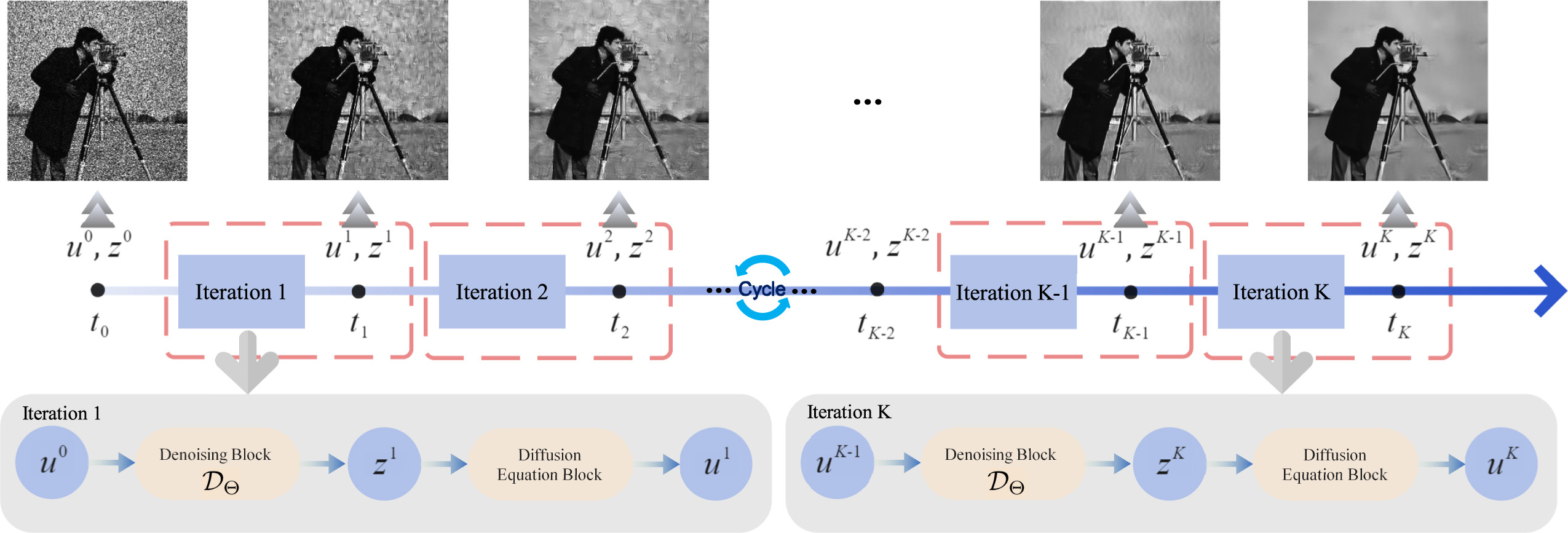 |